A Mechanical Model of
Rod-Shaped Bacteria
Jonas Pleyer
03.02.2025
Overview
| 1. Rod-Shaped Bacteria | (3 slides) |
| 2. Mathematical Model | (9 slides) |
| 3. Computational Algorithms | (5 slides) |
| 4. Parameter Estimation | (3 slides) |
| 5. Outlook | (2 slide) |
Rod-Shaped Bacteria
- One of many bacterial
shapes
- We do not consider coccobacillus (elliptical shape) for now
- Main interest: bacillus
- Length ≈1−10µm, Diameter≈0.5−2µm
- Elongated shape (not simply point-particle) but flexible (Amir et al., 2014)
- Asymmetric growth in direction of long axis
- Why are we interested in this?
⇒ We will get to that later
Rod-Shaped Bacteria
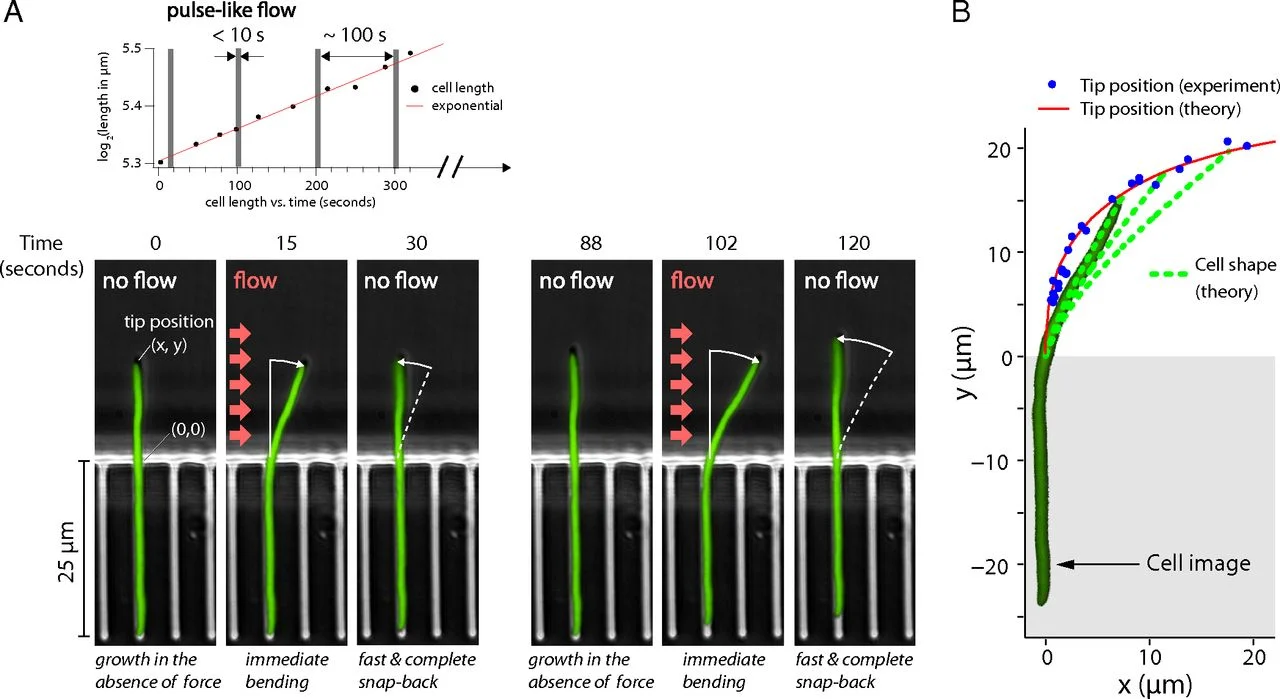
⇒ Anisotropic Mechanical Stress-Driven Differential Growth of Cell Walls
Rod-Shaped Bacteria
Growth of E.Coli
Rod-Shaped Bacteria
State of current models
| ABM/Paper | State |
|---|---|
| Biocellion | Only cylindrical potentials |
| BSim | Supports Rod-Shaped Bacteria; No parameters estimated. |
gro |
⎯⎯⎯ " ⎯⎯⎯ |
| (Martins et al., 2015) | Constructed model but no parameter estimations. |
| (Winkle et al., 2017) | Authors used game engine Chipmunk3D to simulaterods but only studied global phenomena. |
| (Doumic et al, 2020) | Estimated distribution of some parameters (growth rate, length) but no bending and not on individual level. |
⇒ No literature on measuring properties of individual cells!
Mechanics
- Vertices xi connected by springs
- Exert force between two adjacent vertices
ci=xi−xi−1 Fi,springs=−γ(1−∣ci∣l)ci+γ(1−∣ci+1∣l)ci+1
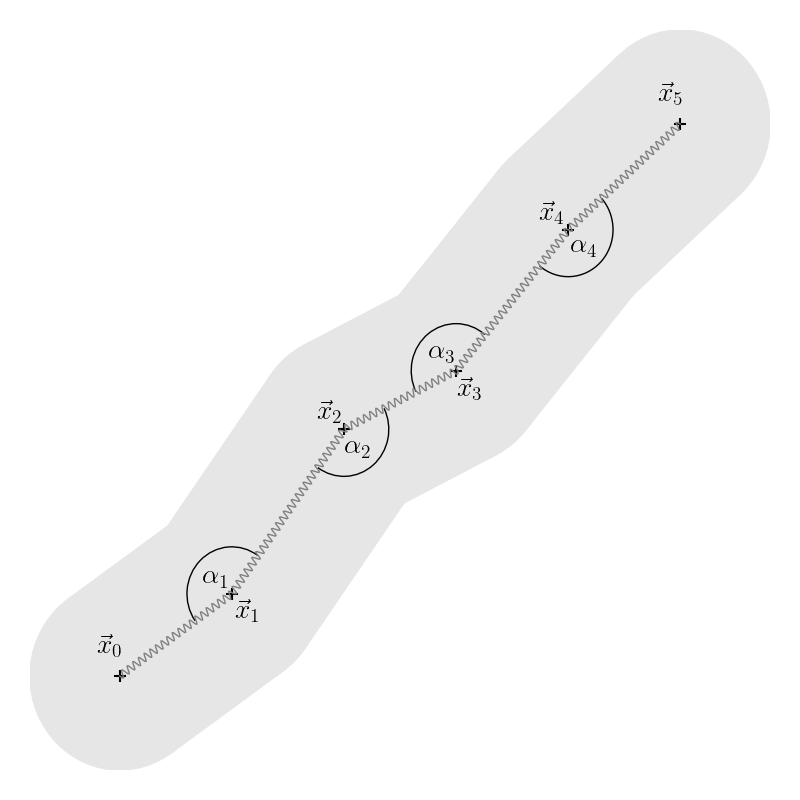
Mechanics

- Bending force acts on vertices xi−1,xi,xi+1
- Proportional to curvature κi at vertex xi
κiFi,curvatureFi−1,curvatureFi+1,curvature=2tan(2αi)=ηκi∣ci−ci+1∣ci−ci+1=−21Fi,curvature=−21Fi,curvature
Mechanics
- Sum all forces
Fi,total=Fi,springs+Fi,curvature+Fi,external
- Integrate equations of motion
∂t2x∂tx=∂tx+2Dξ=Ftotal−λ∂tx
Growth
- Elongation is constant in length growth
(Grover et al., 1977 Rosenberger et al., 1978) - Model as linear growth
∂tl=μ
- For larger collections: introduce phenomenological saturation term depending on number of neighbors n
∂tl=μ(1−Nmin(n,N))
Cell Cycle
- Cell divides in the middle when reaching threshold length lmax
- Calculate new spring lengths
- Calculate new positions of vertices for both cells (interpolate new vertices between vertices of mother-cell)
- (Optional) Pick new growth rate (or other parameters)
Interaction

- Calculate interaction for each vertex xi
- Pointwise to nearest point on ther cells polygon
p=hwj+(1−h)wj+1
for (i, vi) in vertices_cell_1.iter().enumerate() {
// Calculate nearest point, index and segment as above
let (p, j, h) = get_nearest_point_index_segment(&vi, &cell2)?;
// Calculate force between these two points
let calculated_force = cell1.calculate_force_between(&p)?;
// Store calculated force for cell1 and cell2
forces_cell_1[i] += calculated_force;
forces_cell_2[j] -= h * calculated_force;
forces_cell_2[j] -= (1-h) * calculated_force;
}Interaction
Morse-Potential
V(r)=V0(1−e−λ(r−R))2
| Name | Type | ||
|---|---|---|---|
| R | Radius | f32∈R+ |
Fit |
| λ | Stiffness | f32∈R+ |
Fit |
| ζ | Cutoff | f32∈R+ |
Assumption |
| V0 | Strength | f32∈R+ |
Fit |
Interaction
Mie-Potential
U(r)=Cϵ[(rσ)n−(rσ)m]
C=n−mn(mn)n−mn
| Name | Type | ||
|---|---|---|---|
| R | Radius | f32∈R+ |
Fit |
| ϵ | Strength | f32∈R+ |
Fit |
| β | Bound | f32∈R+ |
Assumption |
| ζ | Cutoff | f32∈R+ |
Assumption |
| n,m | Exponents | f32∈R+ |
Fit |
Comparison of Interaction Potentials
Morse
Mie
- Less steep for r→0
- Width of the well affects range and steepness
- Less parameters
- Can represent more types of interactions
- Needs an upper bound for r→0
Variables/Parameters
#[derive(CellAgent, Clone, Debug, Deserialize, Serialize)] pub struct RodAgent { /// Determines mechanical properties of the agent #[Mechanics] pub mechanics: RodMechanics<f32, 3>, /// Determines interaction between agents #[Interaction] pub interaction: RodInteraction<PhysicalInteraction>, /// Rate with which the cell grows pub growth_rate: f32, /// Threshold at which the cell will divide pub division_length: f32, }
#[derive(CellAgent, Clone, Debug, Deserialize, Serialize)] pub struct RodAgent { /// Determines mechanical properties of the agent #[Mechanics] pub mechanics: RodMechanics<f32, 3>, /// Determines interaction between agents #[Interaction] pub interaction: RodInteraction<PhysicalInteraction>, /// Rate with which the cell grows pub growth_rate: f32, /// Threshold at which the cell will divide pub division_length: f32, }
#[derive(CellAgent, Clone, Debug, Deserialize, Serialize)] pub struct RodAgent { /// Determines mechanical properties of the agent #[Mechanics] pub mechanics: RodMechanics<f32, 3>, /// Determines interaction between agents #[Interaction] pub interaction: RodInteraction<PhysicalInteraction>, /// Rate with which the cell grows pub growth_rate: f32, /// Threshold at which the cell will divide pub division_length: f32, }
#[derive(CellAgent, Clone, Debug, Deserialize, Serialize)] pub struct RodAgent { /// Determines mechanical properties of the agent #[Mechanics] pub mechanics: RodMechanics<f32, 3>, /// Determines interaction between agents #[Interaction] pub interaction: RodInteraction<PhysicalInteraction>, /// Rate with which the cell grows pub growth_rate: f32, /// Threshold at which the cell will divide pub division_length: f32, }
#[derive(CellAgent, Clone, Debug, Deserialize, Serialize)] pub struct RodAgent { /// Determines mechanical properties of the agent #[Mechanics] pub mechanics: RodMechanics<f32, 3>, /// Determines interaction between agents #[Interaction] pub interaction: RodInteraction<PhysicalInteraction>, /// Rate with which the cell grows pub growth_rate: f32, /// Threshold at which the cell will divide pub division_length: f32, }
#[derive(Clone, Debug, PartialEq)] pub struct RodMechanics<f32, 3> { /// The current position pub pos: Matrix<f32, Dyn, Const<3>, _>, /// The current velocity pub vel: Matrix<f32, Dyn, Const<3>, _>, /// Controls stochastic motion pub diffusion_constant: f32, /// Spring tension between vertices pub spring_tension: f32, /// Stiffness between two edges pub rigidity: f32, /// Target spring length pub spring_length: f32, /// Daming constant pub damping: f32, }
#[derive(Clone, Debug, PartialEq)] pub struct RodMechanics<f32, 3> { /// The current position pub pos: Matrix<f32, Dyn, Const<3>, _>, /// The current velocity pub vel: Matrix<f32, Dyn, Const<3>, _>, /// Controls stochastic motion pub diffusion_constant: f32, /// Spring tension between vertices pub spring_tension: f32, /// Stiffness between two edges pub rigidity: f32, /// Target spring length pub spring_length: f32, /// Daming constant pub damping: f32, }
#[derive(Clone, Debug, PartialEq)] pub struct RodMechanics<f32, 3> { /// The current position pub pos: Matrix<f32, Dyn, Const<3>, _>, /// The current velocity pub vel: Matrix<f32, Dyn, Const<3>, _>, /// Controls stochastic motion pub diffusion_constant: f32, /// Spring tension between vertices pub spring_tension: f32, /// Stiffness between two edges pub rigidity: f32, /// Target spring length pub spring_length: f32, /// Daming constant pub damping: f32, }
#[derive(Clone, Debug, PartialEq)] pub struct RodMechanics<f32, 3> { /// The current position pub pos: Matrix<f32, Dyn, Const<3>, _>, /// The current velocity pub vel: Matrix<f32, Dyn, Const<3>, _>, /// Controls stochastic motion pub diffusion_constant: f32, /// Spring tension between vertices pub spring_tension: f32, /// Stiffness between two edges pub rigidity: f32, /// Target spring length pub spring_length: f32, /// Daming constant pub damping: f32, }
| Property | Type | ||
|---|---|---|---|
| μ | Growth Rate | f32∈R+ |
Fit |
| lmax | Division Length | f32∈R+ |
Fit |
| xi | Position | Matrix∈Rd×3 |
I.V. |
| vi | Velocity | Matrix∈Rd×3 |
I.V. |
| - | Diffusion | f32∈R+ |
0 |
| l | Spr. Length | f32∈R+ |
I.V. |
| γ | Spr. Tension | f32∈R+ |
Fit |
| η | Rigidity | f32∈R+ |
Fit |
| λ | Damping | f32∈R+ |
Fit |
Numerical Simulation Example
Image Analysis
Time Series of Microscopic Images
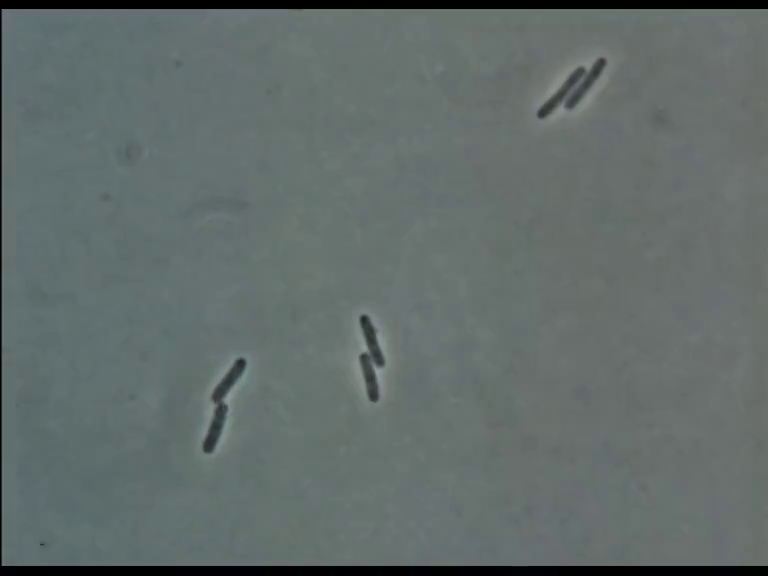
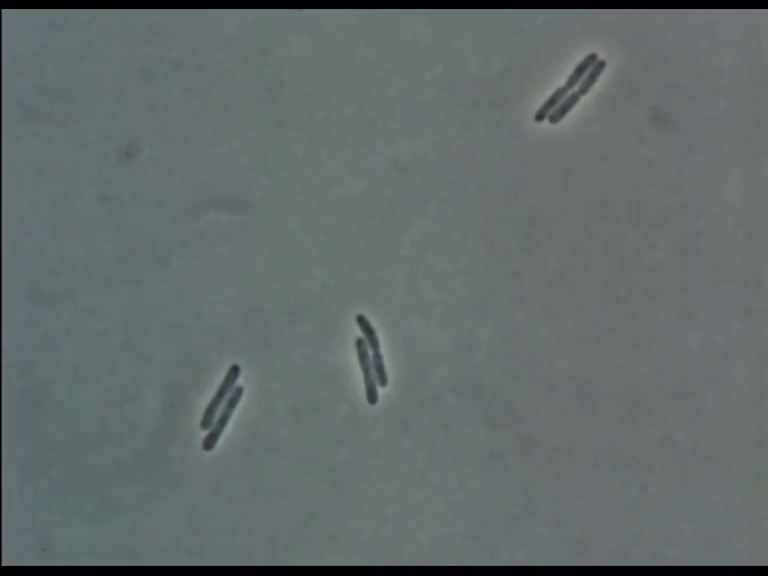
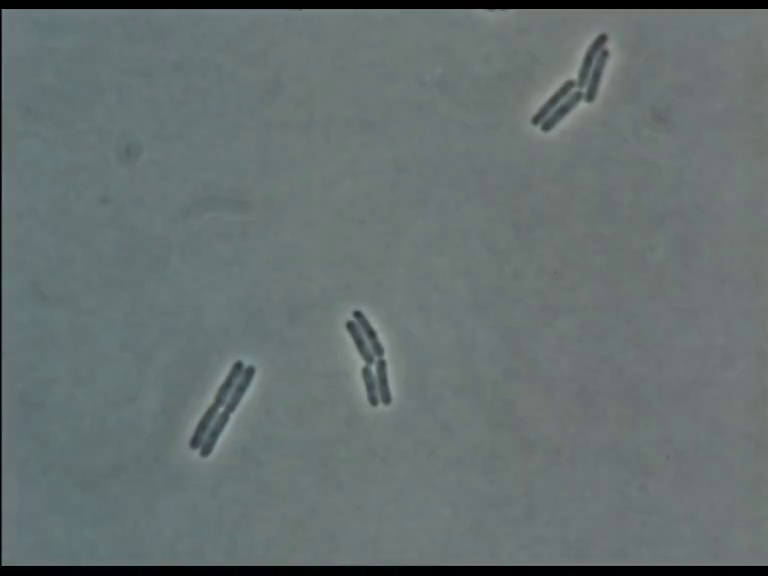
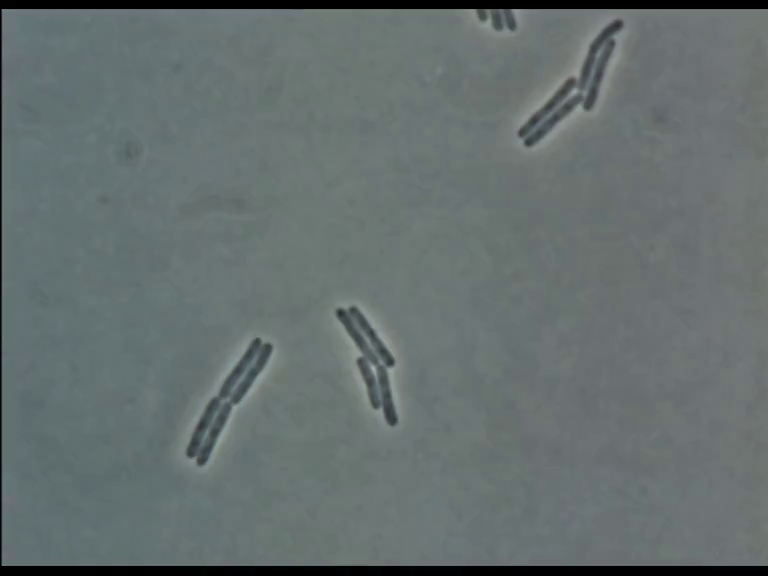
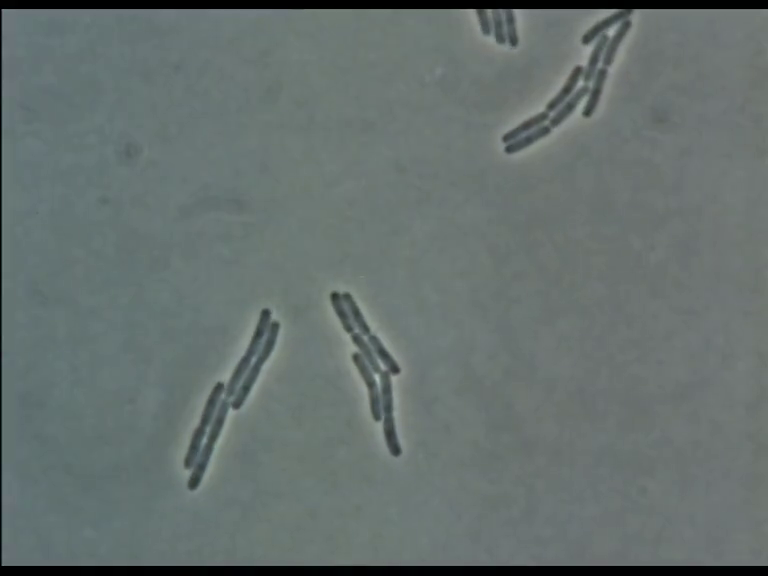
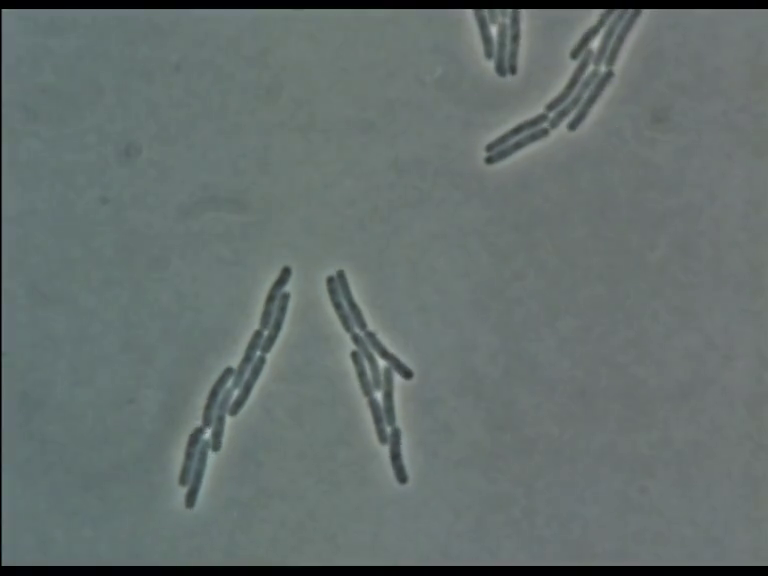
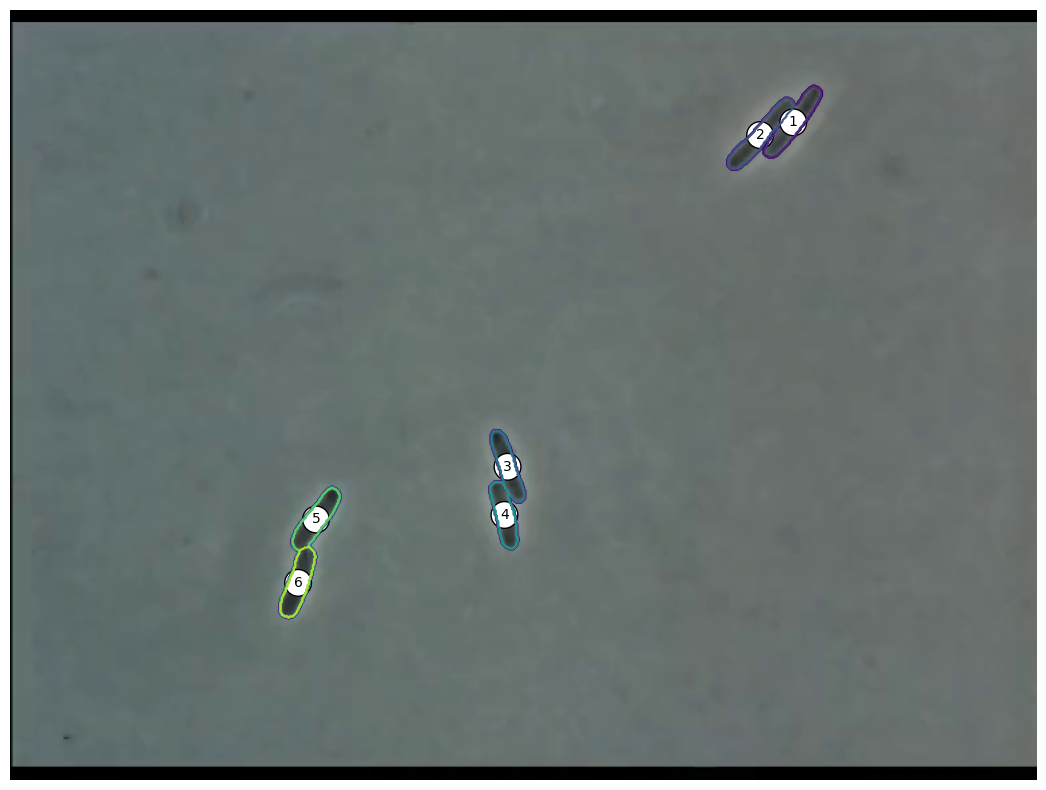
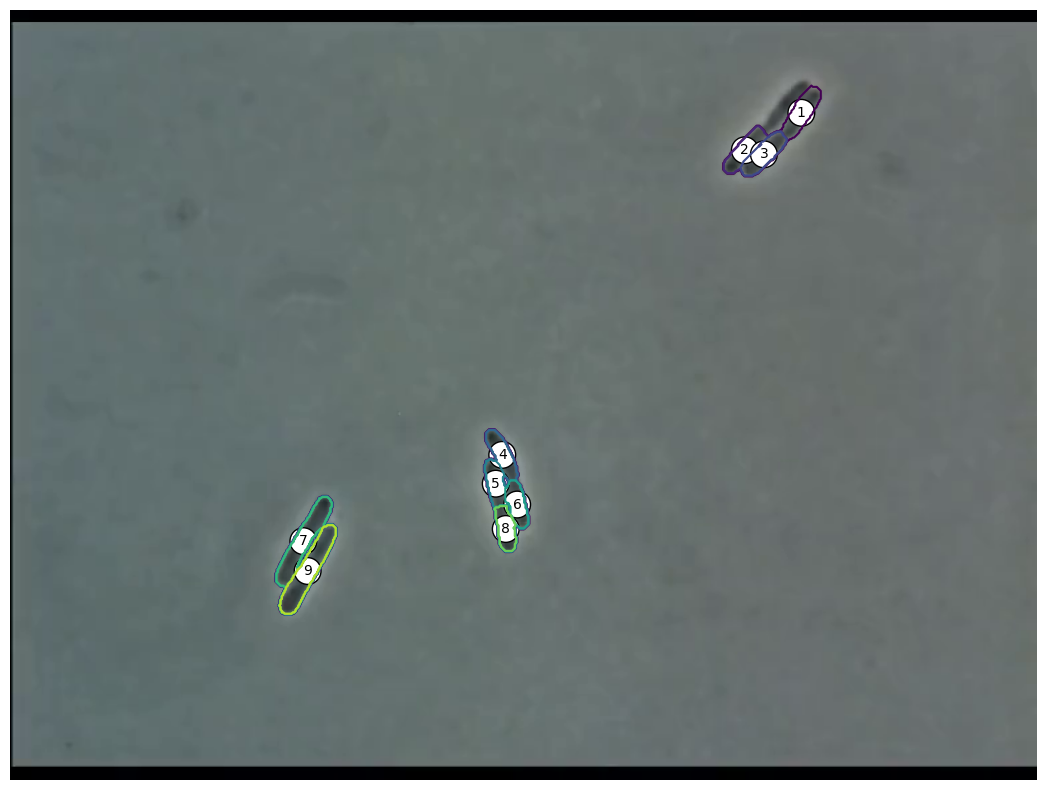

We need methods to map between images
and our numerical simulation
- Extract individual cells from image
✅ (Cell-Segmentation) - Extract positions from individual cell
❌ (No existing algorithm) - Advance simulation
✅ (see implementation of our model) - Compare numerical and real-world results
❓ (what is the cost function?)
Image Analysis
Extracting Positions
Microscopic Image
Cell Masks
Skeletonization
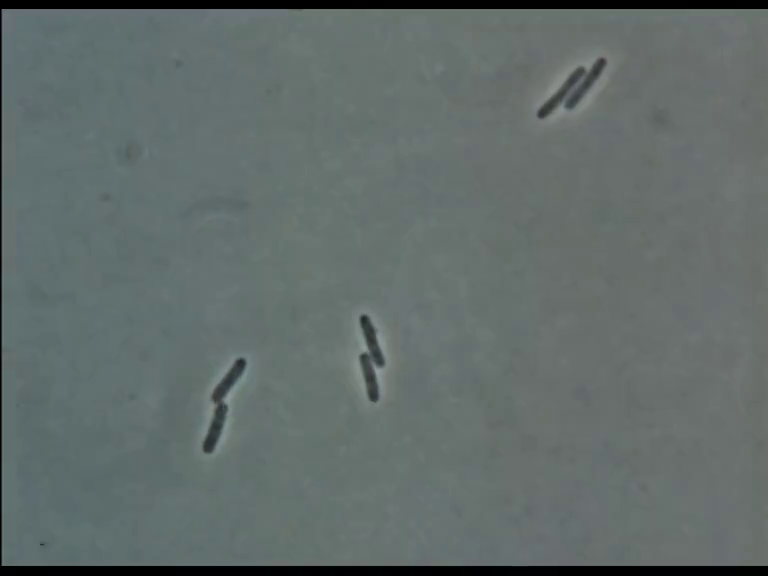

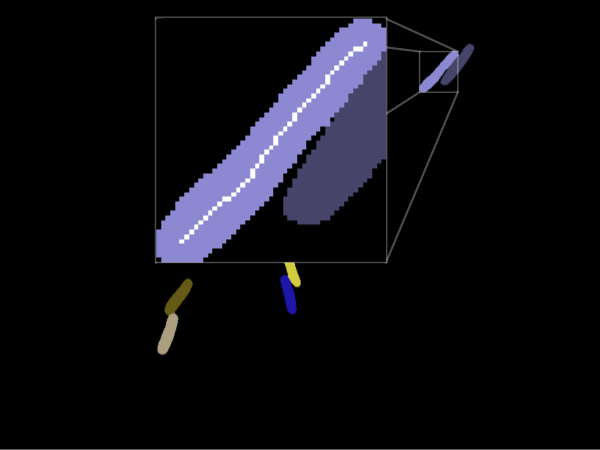
- Take skeleton of cell-mask and interpolate to polygon with N vertices
Image Analysis
Generating Images
- We can use the numerical simulation to generate
artificial data & images - Create masks by projecting 3D image &
assigning unique color to each cell - Use this data to test our position extraction algorithm
Advantage: known input positions




Image Analysis
How to generate Near-Realistic Microscopic Images
- Noise
- Camera Sensor Noise
- Statistic Noise from environmental influences
- Defects
- Lens Aberration
- Dirt on Glass
- etc.
- Lighting (backlight most of the time)
- Cellular properties: reflectivity, luminosity, tranlucency
- Overlapping of bacteria
- Dirt/Other material floating around
⇒ Physically-Based Rendering!

Image Analysis
Extracting Positions



- Crosses show extracted positions
- Lines show actual polygon
- Seems to match quite well
Image Analysis
Extracting Positions
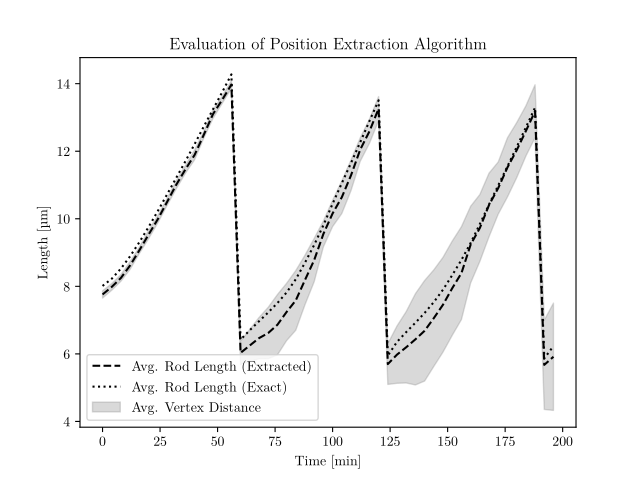
- Measure difference between rod lengths
- Calculate average vertex difference from extracted to known position
- Good agreement with given positions
- In the beginning small underestimation
- In the end small overestimation
Parameter Estimation
Constructing a Cost Function
- Assumption: We have no cell-division
- ⇒ compare euclidean distance between vertices
- If we have cell-division, we need to do something else
Parameter Estimation
Comparing Across Generations




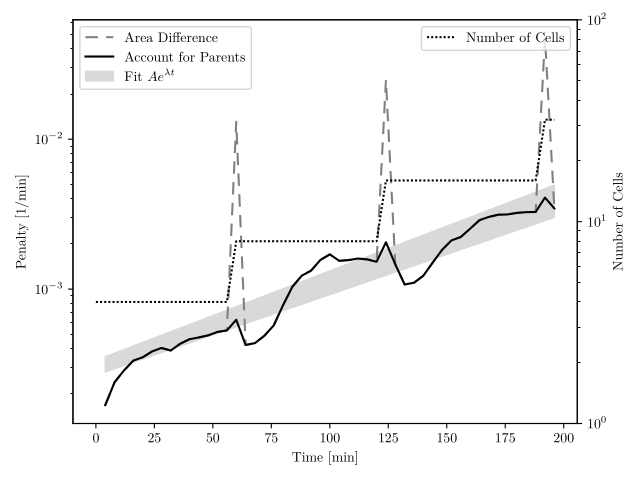
Parameter Estimation
Results
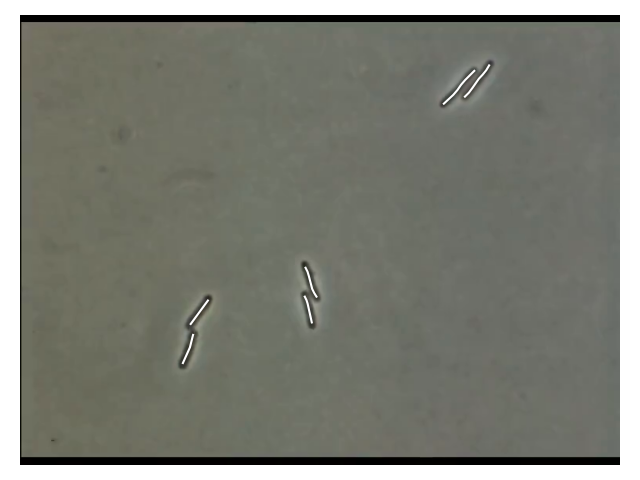
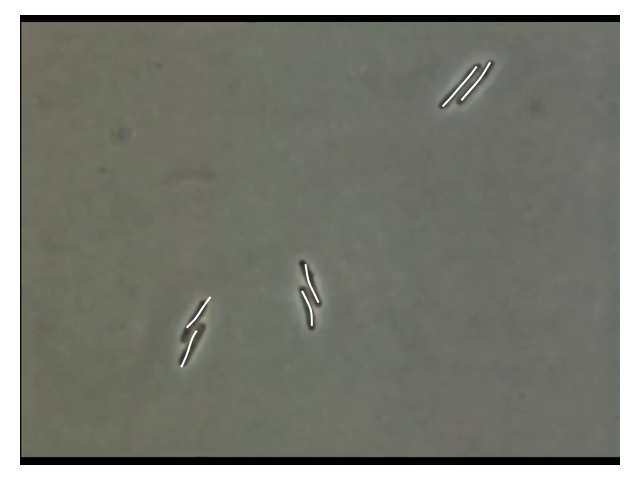
- 2 Pairs are matching well
- Left pair is not aligned very well
⇒ this could be due to the MorsePotentialF32 interaction
potential


Parameter Estimation
Results
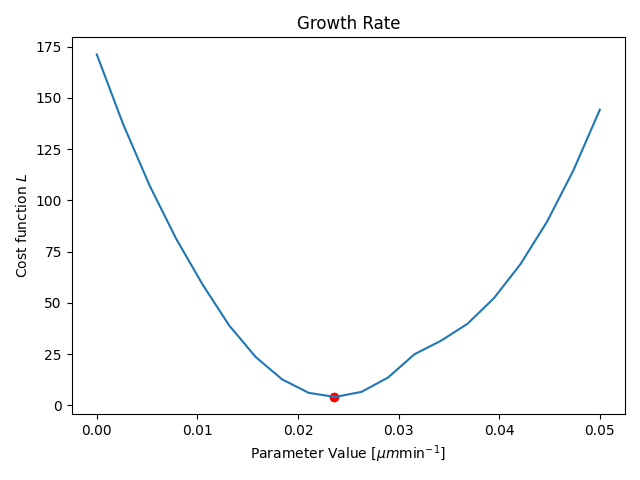
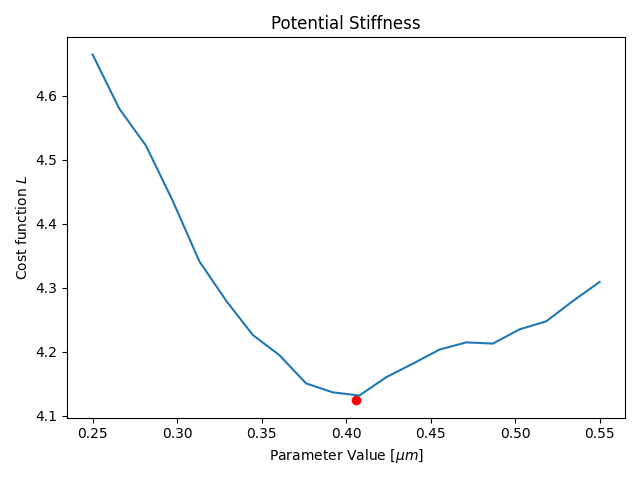
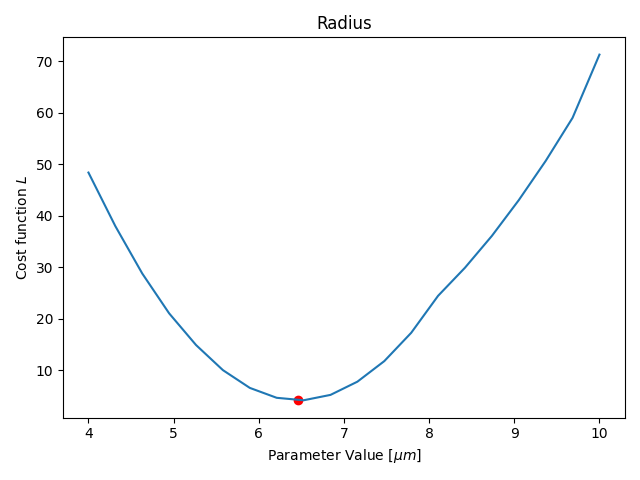
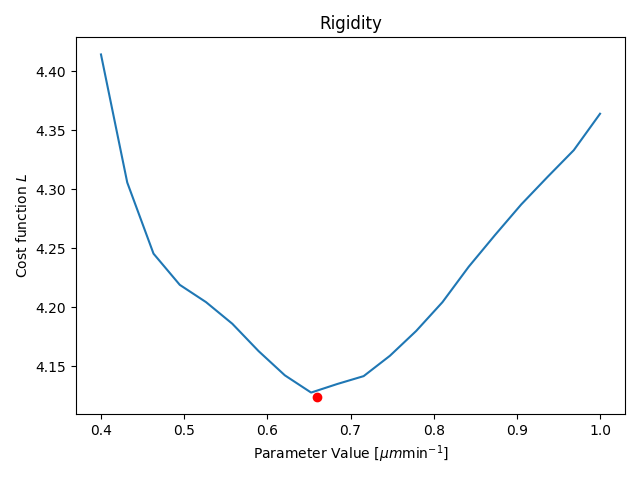
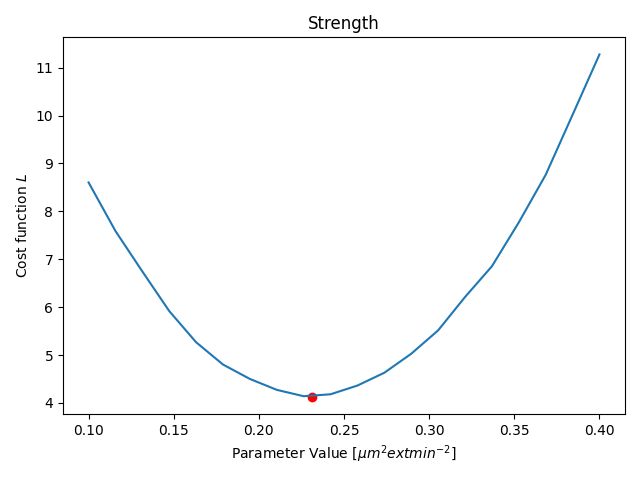
- Only one parameter for all agents (not individual)
- Only one time-step is fitted
- Duration: ≈15min (depending on your hardware)
Parameter Estimation
Optimization Strategies
- Estimate parameters for each time-step
- Run simulation over multiple time-steps and compare results
- option to rebase every n time-steps and start with new initial conditions
- Global vs Local optimization
- unfortunately in general not possible to calculate Jacobian
Python Package
pip install cr_mech_coliimport cr_mech_coli as crm # Configure inputs config = crm.Configuration() agent_settings = crm.AgentSettings() # Run simulation cell_container = crm.run_simulation( config, agent_settings, ) # Render Images render_settings = crm.RenderSettings() crm.store_all_images( cell_container, config.domain_size, render_settings )
import cr_mech_coli as crm # Configure inputs config = crm.Configuration() agent_settings = crm.AgentSettings() # Run simulation cell_container = crm.run_simulation( config, agent_settings, ) # Render Images render_settings = crm.RenderSettings() crm.store_all_images( cell_container, config.domain_size, render_settings )
import cr_mech_coli as crm # Configure inputs config = crm.Configuration() agent_settings = crm.AgentSettings() # Run simulation cell_container = crm.run_simulation( config, agent_settings, ) # Render Images render_settings = crm.RenderSettings() crm.store_all_images( cell_container, config.domain_size, render_settings )
import cr_mech_coli as crm # Configure inputs config = crm.Configuration() agent_settings = crm.AgentSettings() # Run simulation cell_container = crm.run_simulation( config, agent_settings, ) # Render Images render_settings = crm.RenderSettings() crm.store_all_images( cell_container, config.domain_size, render_settings )
import cr_mech_coli as crm # Configure inputs config = crm.Configuration() agent_settings = crm.AgentSettings() # Run simulation cell_container = crm.run_simulation( config, agent_settings, ) # Render Images render_settings = crm.RenderSettings() crm.store_all_images( cell_container, config.domain_size, render_settings )


Documentation
Outlook
- Cell-Segmentation & Cell-Tracking
- Generate Dataset of near-realistic images with masks
- Asses if this can improve existing Cell-Segmentation tools
- This allows us to easily study Cell-Tracking solutions
- Distribution of Parameters
- Can we fit enough cells individually simultanously?
- How are parameters of cells distributed?
- Inheritance of Parameters
- Will our algorithms work over multiple bacteria generations?
- How are parameters inherited to daughter cells?
We are meeting up with Alexander Rohrbach
this week to discuss how to take things further.